Посчитать IRR без Excel? Такое возможно!

В первой части нашей трилогии мы размышляли о природе IRR и механике её расчёта с помощью Microsoft Excel.

Теперь обсудим, как быть, если у вас под рукой не оказалось экселя, а руки так и чешутся посчитать IRR? Выход есть: существует техника расчёта IRR «на бумаге», которой, например, необходимо уверенно владеть для успешной сдачи экзаменов по программе АССА «Введение в Финансы и управление бизнесом» и «Финансовый менеджмент».

Чтобы раскрыть все тонкости расчёта IRR «на бумаге», нам придётся напомнить себе про основу основ оценки инвестиционных проектов – чистую приведённую стоимость (NPV).

Взаимосвязь NPV и IRR

NPV используется для оценки приемлемости инвестиционного проекта и представляет собой разницу между дисконтированной стоимостью денежных потоков проекта (PV) и размером первоначальных инвестиций.

NPV – это сугубо экономический показатель, его не стоит воспринимать как измеритель живых денег, которые можно положить в сейф.

NPV в отличие от IRR, учитывает как денежные потоки проекта, так и минимальную требуемую инвесторами доходность, именуемую как стоимость капитала или ставка дисконтирования.

Вернемся снова к нашему проекту из первой части трилогии. Вот его ожидаемые денежные потоки:

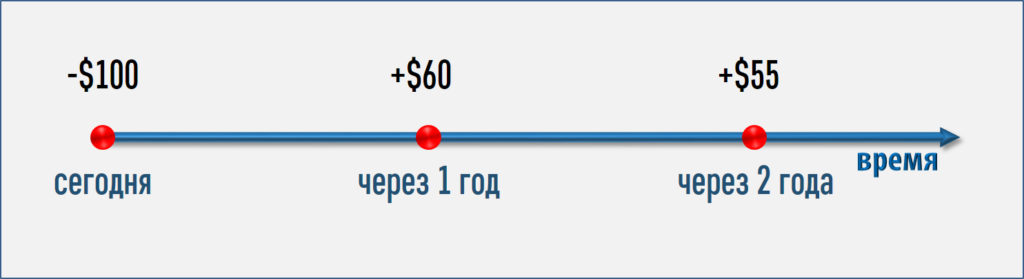
Если минимальная требуемая инвесторами доходность равна 8% годовых (т.е. они готовы инвестировать в наш проект при ожидаемой доходности на уровне 8% годовых и выше), то идеально правильный расчёт NPV будет таким:

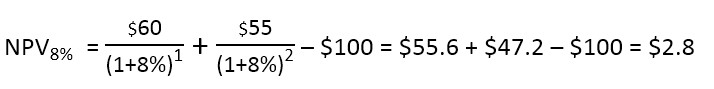
или с помощью доступных на экзамене ACCA коэффициентов дисконтирования:

NPV_8% = $60 × 0.926 + $55 × 0.857 — $100 = $55.6 + $47.1 – $100 = $2.7

Разница в значениях ($2.7 против $2.8) вызвана исключительно округлением, и я предлагаю остановиться на $2.7. Вы же не забыли, что экселя у нас по-прежнему под рукой нет?

В любом случае, NPV нашего проекта положительна, а, значит, он финансово привлекателен и обеспечивает требуемую инвесторами доходность в 8% годовых. Если бы инвесторы требовали не менее 14% (например, из-за возросших валютных рисков) то NPV нашего проекта составила бы:

или с помощью доступных на экзамене ACCA коэффициентов дисконтирования:

NPV_14% = $60 × 0.877 + $55 × 0.769 — $100 = $52.6 + $42.3 – $100 = ($5.1)

Оказалось, что при требуемой доходности 14%, наш проект уже непривлекателен. Нетрудно заметить, что чем выше требуемая инвесторами доходность (ставка дисконтирования), тем ниже NPV проекта.

Как мы уже выяснили в первой части нашей трилогии: IRR – это годовая доходность проекта. Если NPV проекта положительна, то он финансово приемлем. Каковы были требования инвесторов по нашему проекту? Инвесторы требовали доходность не менее 8% годовых. Значит, IRR нашего проекта явно больше 8%, раз NPV получилась положительной. А вот если бы инвесторы требовали не менее 14% годовых, то наш проект для них уже невыгоден, так как NPV отрицательная. Выходит, IRR нашего проекта явно больше 8%, но меньше 14%.

Помните, что IRR — результат денежных потоков проекта, а стоимость капитала — это минимальная требуемая инвесторами доходность, которая используется как исходная ставка дисконтирования для оценки NPV.

Теперь давайте сделаем несложное умозаключение о связи между NPV c одной стороны, и IRR и стоимости капитала с другой:

Вот мы и добрались до научного толкования IRR: это ставка дисконтирования, при которой NPV равна нулю. Это вовсе не значит, что считая IRR мы «обнуляем» фактическую NPV проекта. NPV проекта такова, какой ей велят быть денежные потоки проекта и применимая к проекту стоимость капитала.

Собственно техника расчёта, или «поляции»

Расчёт IRR «на бумаге» сводится к поиску ставки дисконтирования, при которой NPV равна нулю. Это поиск именуется как метод интер- или экстраполяции. Не стоит ругаться этими словами, если вас попросили посчитать IRR проекта на работе: помните, что для практики есть как минимум Excel.

Расчёт IRR «на бумаге» можно разделить на два последовательных шага:

Шаг 1. Определить связь между NPV проекта и ставкой дисконтирования

Шаг 2 Используя связь из Шага 1, «подобрать» ставку, при которой NPV равна нулю.

Схематично это выглядит так:

Итак, нам нужны две ставки и два соответствующих значения NPV. Мы уже знаем, что при ставке 8% NPV нашего проекта $2.7, а при 14% — ($5.1). Обратите внимание: как мы уже отмечали в нашей первой части: IRR определяется исключительно денежными потоками. Ставки, которые мы использовали (8% и 14%) произвольны. Мы с тем же успехом могли бы использовать, скажем, 2% и 10%. Правда, результат будет немного иным – но об этом я пока умолчу.

Теперь есть всё, чтобы найти IRR. Классическая формула нахождения IRR «на бумаге» выглядит так:

r_м – мéньшая из двух используемых ставок дисконтирования;

r_б – бóльшая из двух используемых ставок дисконтирования;

NPV_м – значение NPV при мéньшей ставке дисконтирования;

NPV_б – значение NPV при бóльшей ставке дисконтирования.

Если вы из тех счастливчиков, кто готовится к сдаче экзаменов по программе ACCA, то у меня для вас плохая и хорошая новости. Начнем с плохой: этой монструозной формулы расчёта IRR нет среди подсказок, которыми вы официально можете пользоваться на экзамене.

Ну, а теперь хорошая: из каждой ситуации есть выход. Зубрить такого монстра не вариант, поэтому предлагаем решение, в основе которого обычная пропорция времён средней школы.

Поиск IRR расчётным путем выглядит так:

Обобщить это видео можно такой таблицей:

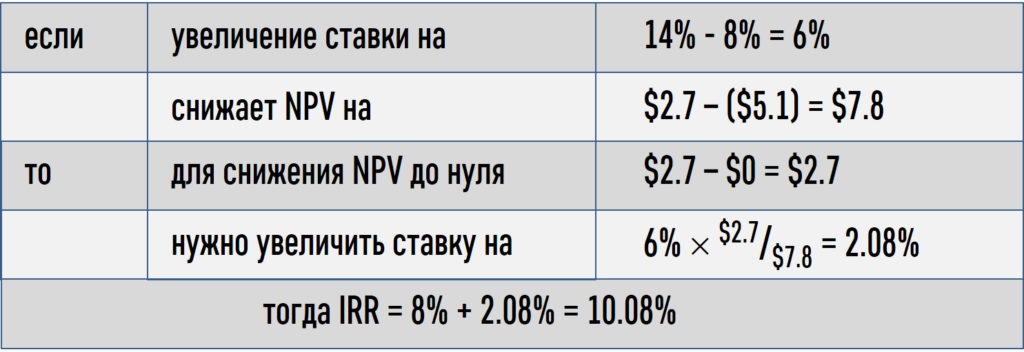
В принципе, это не генная инженерия. Но в отличие от использования функций в Excel, результат нашего расчёта «на бумаге» очень сильно зависит от выбранных ставок.

Если бы мы выбрали ставки в 4% (NPV была бы равна $8.5) и 6% (NPV была бы равна $5.6), то IRR нашего проекта оказалась бы такой:

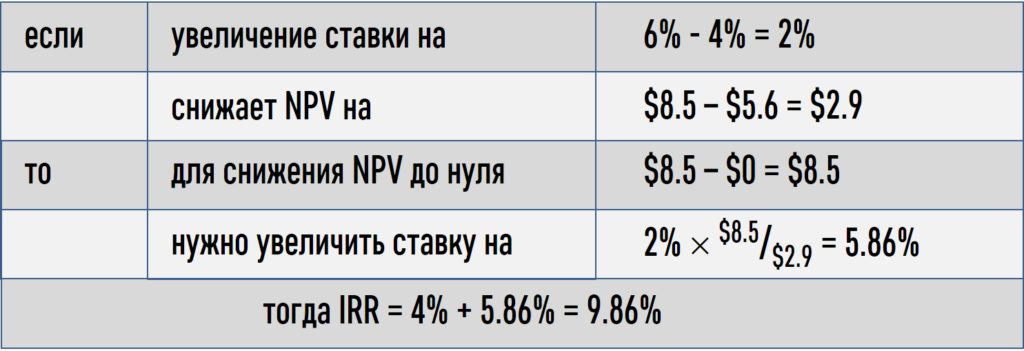
Смотрите-ка, что вышло: при использовании одной произвольной пары ставок (8% и 14%) в первом расчёте IRR получилась равной 10.08%, а при использовании другой произвольной пары (4% и 6%) во втором – 9.86%. А ведь мы-то знаем, что точное значение IRR – ровно 10% годовых. Знаем, потому что с помощью функции ВСД посчитали его в первой части нашей трилогии!

То есть рассчитать IRR «на бумаге» реально, однако результат будет зависеть от используемых ставок. Почему? Потому, что этот метод наивно полагает, что между NPV и ставкой дисконтирования линейная зависимость, то есть при каждом изменении ставки на 1% NPV каждый раз меняется на одну и ту же величину.

В действительности же никакой линейной зависимости нет. Вот оно, реальное поведение NPV при изменении ставки:

Вы можете пожать плечами — мол, какое это имеет значение? Всё равно почти 10%.

Ну, представьте, если в жизни ставка растёт с 30% до 31%. Многие инвесторы могут такое событие и вовсе пропустить мимо.

На низких же уровнях, напротив, изменения ставки могут быть очень значимы для результата. Представьте, что ставка меняется с 2% до 3%. Это уже в целых 1.5 раза! Сегодня, когда процентные ставки на рекордно низких уровнях, инвесторы как никогда пристально следят за заседаниями финансовых регуляторов, на которых принимаются решения об изменении ключевых ставок. Изменение ставок с низких уровней всего на десятые проценты способно сильно взбудоражить финансовые рынки.

Увы, этот недостаток бумажного метода расчёта IRR ограничивает его применение только финансовыми экзаменами ACCA, где требуется продемонстрировать, что вы понимаете логику IRR. А в жизни повода использовать метод «поляции» у вас не представится. Ну, может, только если только вы клавиатуру ноутбука зальёте чаем.

Но есть и ещё один подводный камень: не без недостатка и сама IRR. Недостаток у неё врожденный и в определенных случаях может сбить инвесторов с толку. Об этом недостатке и способах борьбы с ним мы поговорим в третьей части нашей трилогии.

Продолжение следует…

Вход

Посчитать IRR без Excel? Такое возможно!

Евгений Кромский продолжает Трилогию об IRR. Эпизод 2: Расчёт IRR на бумаге

Взаимосвязь NPV и IRR

Собственно техника расчёта, или «поляции»

Евгений Кромский

1 - комментарии к теме "Посчитать IRR без Excel? Такое возможно!"

Оставить сообщение Отменить ответ

ПОДПИСКА НА СТАТЬИ

ТОЛКОВЫЙ ОНЛАЙН-СЛОВАРЬ

ТЕРМИНЫ ОНЛАЙН-СЛОВАРЯ

СВЕЖИЕ КОММЕНТАРИИ

Мы обновили учебник ДипИФР к декабрю 25го

Мы в отличной форме

Набор на осеннюю сессию русскоязычной АССА

Вышел видео-курс "Бухгалтерский учёт по МСФО"